Identifying microstates on the group level (second level clustering)
When performing cluster analyses in a series of EEG, the resulting individual microstate class maps have no particular order, and may also vary in polarity. Thus,we cannot simply average the microstate class maps across EEGs, but we need to permute the maps obtained within each EEG in a way that maximized the commonality across cases before. This results in a second clustering problem, this time with the constraint that there is a one-to-one relationship of the individual microstate class maps in each EEG and the mean microstate class maps.
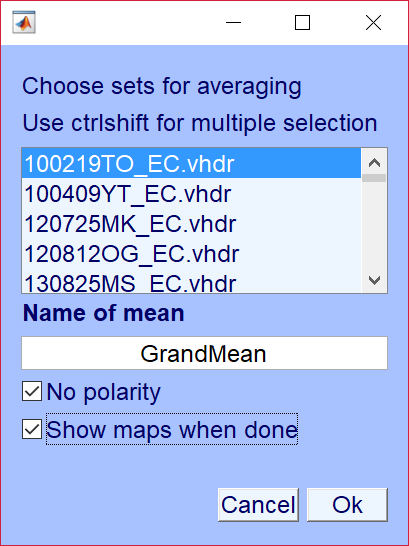
The computation of mean microstate class maps on this second level is accessed thru the menu "Tools->Microstates->Compute mean microstate maps across individuals". You can also use the same tool to average across mean microstate class maps thru the menu item "Tools->Microstates->Compute grand mean microstate maps across means". The dialog looks like this:
Alternatively, the analysis step can also be started on the command line or using a script. In this case, the function to be called is
[EEG,com] = pop_CombMSTemplates(ALLEEG, Index, DoMeans, ShowWhenDone, MeanSetName, IgnorePolarity);
typically followed by
[ALLEEG, EEG, CURRENTSET] = pop_newset(ALLEEG, EEG, numel(ALLEEG)+1,'gui','off');
where the ALLEEG contains all EEG data, EEG is the data structure with the obtained clusters, com is a string with the command necessary to replicate the computation, Index indicates which elements of ALLEEGs are to be used for the averaging, ShowWhenDone allows an immediate display of the resulting mean microstate class maps, MeanSetName is the name of the new EEG dataset, and IgnorePolarity makes the algorithm to flip (multiply by -1) some maps for a better commonality. The DoMeans allows you to select if you want to average individual microstate class maps (= 0), or to opt for the averaging of mean microstate class maps (= 1).